Day 50
Today was the 2nd day for the test. I was surprised by how many students took the full period to continue working on it. I spent the entire time going from one student to the next answering questions or telling them that, no, they hadn't actually finished the test. I hope they are seeing how much more they accomplish by not giving up. Those who did finish early got to work on some (fun) Balance Benders like these:
(This is a level 3 one; they had easier ones too.)
Day 51
I am posting for tomorrow as I will be working with the awesome Alex Overwijk (@AlexOverwijk) and Sheri Walker and therefore not at my school. I had planned on doing Barbie Bungee next, but I didn't want to leave that for my supply teacher so I thought they could work more easily on some algebra in my absence.
This is followed by a few practice examples.
Part V will hopefully help students start to make connections between standard and factored form. Hopefully...
I am not thrilled with this. However, my students will need these skills so this is what I came up with. I welcome suggestions for improvement.
Meanwhile, I am making duct tape dresses for my Barbies which is creating a lot of talk about me in the math/English office!
Tuesday 29 April 2014
Monday 28 April 2014
MFM2P - Day 49
Day 49
Today was test day. Perhaps it should not, but it surprised me how many students walked in and said "Do we have a test today?". One even said "Do you hate us that much that you would have a test on a Monday?". This kind of comment makes me sad. I wish they didn't view tests as punishment. Or as something to be feared. I was surprised by the anxiety level of some students this time around. Time isn't an issue - they get a second class to finish up, if needed. They can work on material in between the two days - I am completely in favour of them doing more math outside of class. But still, I find myself being something of a cheerleader - encouraging them when they say they have no idea what to do, pointing them in the right direction until that light bulb goes on and they say "Yeah, I got it.". They will persevere. But only because I make them.
The thing about tests with this class is that I will not accept a completely wrong or blank answer. Traditionally, if a student does this then they lose all the marks for that question (or don't get any marks, depending on how you think about it). Often, you know that a student knows more than they are showing you, which must be frustrating for them. However, in my MFM2P class I prompt them until they get to a point where they know what to do. Sometimes that even involves working through a similar example. I do this all in a pink or orange pen so that I know what I have helped them with when I mark (level) the test. The result is that I think I see a more complete picture of what they have learned and are able to do.
I hope that by the end of the semester they will be more confident in their work. That they will be willing to try to answer questions even if they aren't sure they are going down the right path. That they will be proud of all the math they will be able to do and that they can apply some of that to real life situations. It's a hard sell, but I'll keep trying.
Today was test day. Perhaps it should not, but it surprised me how many students walked in and said "Do we have a test today?". One even said "Do you hate us that much that you would have a test on a Monday?". This kind of comment makes me sad. I wish they didn't view tests as punishment. Or as something to be feared. I was surprised by the anxiety level of some students this time around. Time isn't an issue - they get a second class to finish up, if needed. They can work on material in between the two days - I am completely in favour of them doing more math outside of class. But still, I find myself being something of a cheerleader - encouraging them when they say they have no idea what to do, pointing them in the right direction until that light bulb goes on and they say "Yeah, I got it.". They will persevere. But only because I make them.
The thing about tests with this class is that I will not accept a completely wrong or blank answer. Traditionally, if a student does this then they lose all the marks for that question (or don't get any marks, depending on how you think about it). Often, you know that a student knows more than they are showing you, which must be frustrating for them. However, in my MFM2P class I prompt them until they get to a point where they know what to do. Sometimes that even involves working through a similar example. I do this all in a pink or orange pen so that I know what I have helped them with when I mark (level) the test. The result is that I think I see a more complete picture of what they have learned and are able to do.
I hope that by the end of the semester they will be more confident in their work. That they will be willing to try to answer questions even if they aren't sure they are going down the right path. That they will be proud of all the math they will be able to do and that they can apply some of that to real life situations. It's a hard sell, but I'll keep trying.
Thursday 24 April 2014
MFM2P - Days 47 & 48
Day 47
This will be a short post. We did the last example from the solving by substitution set and then students worked on the review package I put together to prepare for Monday's test. I worked with them in small groups and answered individual questions. Trig is still what they have the most trouble remembering. But they do get it once they are pointed in the right direction. Still, I think I need to do more next time around.
Day 48
I'm cheating and posting for tomorrow but half of my class will be on a field trip and we will be doing more review work. If anything exciting happens, I'll be sure to update!
And since Dan Meyer liked the last post in which I added a picture of my dogs, here is one of them again, on the last of the snow for the season.
This will be a short post. We did the last example from the solving by substitution set and then students worked on the review package I put together to prepare for Monday's test. I worked with them in small groups and answered individual questions. Trig is still what they have the most trouble remembering. But they do get it once they are pointed in the right direction. Still, I think I need to do more next time around.
Day 48
I'm cheating and posting for tomorrow but half of my class will be on a field trip and we will be doing more review work. If anything exciting happens, I'll be sure to update!
And since Dan Meyer liked the last post in which I added a picture of my dogs, here is one of them again, on the last of the snow for the season.
Wednesday 23 April 2014
MFM2P - Day 46
Day 46
Estimation 180... Mr. Stadel's height compared to a bus & clearance height of garage, then angle or percentage of pie eaten. A few students had answers that didn't make sense but changed them when I pointed something out about the picture. For example, for this picture:
one student had a guess of 80%. I mentioned that we all knew the amount eaten should be more than 50%, which was enough for that student to realize that it should also be less than 75%.
After our estimating, we moved on to solving systems of linear equation by substitution. Well, we did it more than one way. Here was the first example:
My students make sense of problems by looking at data. It's a concrete starting point for them. So they looked data which wasn't going up very quickly. I suggested going up by more than 1 student at a time.
We got to our solution numerically pretty quickly. Great. How does this connect graphically? They graphed by hand; I graphed in Desmos:
We talked about what the break even point meant and why it is important to know the break even point before an event. Then we tackled the problem algebraically. We started by creating equations to model the situation, then solved the system:
There we go - solved numerically, graphically and algebraically. They worked through this at their own pace - those who were done quickly moved on to the next question. Some didn't see the advantage of solving this algebraically but it quickly became apparent with question 3:
None of my students found the solution numerically. They could estimate graphically (if graphing by hand), but algebra allowed them to find the exact solution.
That's it - 2 questions today, but lots of good mathematical connections going on. This is how we are ending cycle 2. We will work on review questions tomorrow. There is a big field trip on Friday for those students taking history so the test will be on Monday.
Estimation 180... Mr. Stadel's height compared to a bus & clearance height of garage, then angle or percentage of pie eaten. A few students had answers that didn't make sense but changed them when I pointed something out about the picture. For example, for this picture:
one student had a guess of 80%. I mentioned that we all knew the amount eaten should be more than 50%, which was enough for that student to realize that it should also be less than 75%.
After our estimating, we moved on to solving systems of linear equation by substitution. Well, we did it more than one way. Here was the first example:
My students make sense of problems by looking at data. It's a concrete starting point for them. So they looked data which wasn't going up very quickly. I suggested going up by more than 1 student at a time.
We got to our solution numerically pretty quickly. Great. How does this connect graphically? They graphed by hand; I graphed in Desmos:
We talked about what the break even point meant and why it is important to know the break even point before an event. Then we tackled the problem algebraically. We started by creating equations to model the situation, then solved the system:
There we go - solved numerically, graphically and algebraically. They worked through this at their own pace - those who were done quickly moved on to the next question. Some didn't see the advantage of solving this algebraically but it quickly became apparent with question 3:
None of my students found the solution numerically. They could estimate graphically (if graphing by hand), but algebra allowed them to find the exact solution.
That's it - 2 questions today, but lots of good mathematical connections going on. This is how we are ending cycle 2. We will work on review questions tomorrow. There is a big field trip on Friday for those students taking history so the test will be on Monday.
Tuesday 22 April 2014
MFM2P - Day 45
Day 45
I'm starting to jump around the Estimation 180 site. My students still enjoy it so we keep doing it. Today we did a variety - one song length, one number of carts, one distance between two cities and one number of pennies to form a shape. I realize that they can't use previous estimations to help with the new ones when I do this, but I will go back and do more of each.
Back to equations of lines. We worked on slope last week and today we started by writing the equation of a line given its slope and y-intercept. We had to back up and define y-intercept first (several times) and doing this exercise abstractly was likely not a great idea. I'm not sure that everything needs to be in context, but I think I could have done a better job of tying it all together. The next examples were graphical - again, finding the equation of the line. At least this gave some meaning to the slope and y-intercept.
Next, we tackled our first "solving by substitution" question:
This took a long time. The rest of the period, in fact. We came up with equations, looked at some data, sketched graphs, made sure we understood what we were trying to find, then had to use algebra to solve. Algebra. Sometimes it seems like they have never done it before. But we did get through it and may be in good shape to try more similar problems tomorrow.
I'm starting to jump around the Estimation 180 site. My students still enjoy it so we keep doing it. Today we did a variety - one song length, one number of carts, one distance between two cities and one number of pennies to form a shape. I realize that they can't use previous estimations to help with the new ones when I do this, but I will go back and do more of each.
Back to equations of lines. We worked on slope last week and today we started by writing the equation of a line given its slope and y-intercept. We had to back up and define y-intercept first (several times) and doing this exercise abstractly was likely not a great idea. I'm not sure that everything needs to be in context, but I think I could have done a better job of tying it all together. The next examples were graphical - again, finding the equation of the line. At least this gave some meaning to the slope and y-intercept.
Next, we tackled our first "solving by substitution" question:
This took a long time. The rest of the period, in fact. We came up with equations, looked at some data, sketched graphs, made sure we understood what we were trying to find, then had to use algebra to solve. Algebra. Sometimes it seems like they have never done it before. But we did get through it and may be in good shape to try more similar problems tomorrow.
Thursday 17 April 2014
MFM2P - Day 44
Day 44
Today was some of my students' favourite class. Nothing to do with math, of course. My students got hot chocolate this morning. They were so well-behaved and patient waiting to get their cup ready - it was awesome. Some had mints which they added to make it more "sophisticated"! They politely asked for seconds and they very nicely said thank you. It was a good thing. And we did the Easter Estimation 180's while they drank it.
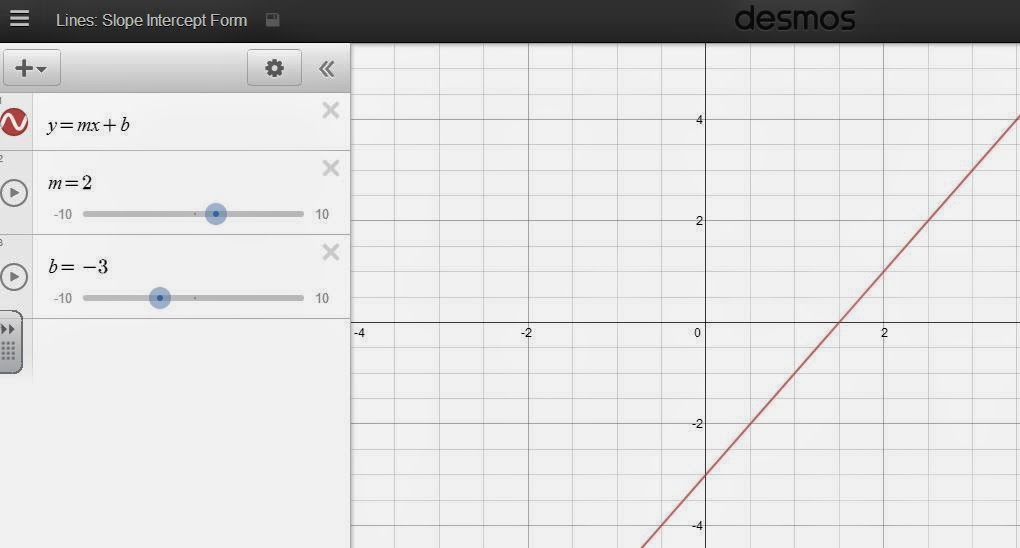
With a few groans we moved back to working on slope. I circulated helping them with the worksheet from yesterday. Many were getting the hang of finding the change in y and the change in x and some were finding the ratio correctly too. They needed a little help with the "special" slopes - those of horizontal and vertical lines. Hopefully emphasizing that a horizontal line is not steep at all helps make the right connection to a slope of 0. Some students had trouble finding the slope between two points (without a graph) but did pretty well once I pointed them to their comp books where we had done a couple of examples yesterday. Some issues that came up were getting the ratio the right way around and simplifying, but I did not see any student mixing up x-values and y-values (yay!). This work took a while but was worthwhile. We finished the day by looking at line graphs on Desmos. I entered y = mx + b and added sliders for m and b then moved them so the students could see the effect. Here is the ready-made example available in Desmos:
They may not have made all the connection I want them to yet, but this plants the seed for the work we will do on Tuesday.
Today was some of my students' favourite class. Nothing to do with math, of course. My students got hot chocolate this morning. They were so well-behaved and patient waiting to get their cup ready - it was awesome. Some had mints which they added to make it more "sophisticated"! They politely asked for seconds and they very nicely said thank you. It was a good thing. And we did the Easter Estimation 180's while they drank it.
With a few groans we moved back to working on slope. I circulated helping them with the worksheet from yesterday. Many were getting the hang of finding the change in y and the change in x and some were finding the ratio correctly too. They needed a little help with the "special" slopes - those of horizontal and vertical lines. Hopefully emphasizing that a horizontal line is not steep at all helps make the right connection to a slope of 0. Some students had trouble finding the slope between two points (without a graph) but did pretty well once I pointed them to their comp books where we had done a couple of examples yesterday. Some issues that came up were getting the ratio the right way around and simplifying, but I did not see any student mixing up x-values and y-values (yay!). This work took a while but was worthwhile. We finished the day by looking at line graphs on Desmos. I entered y = mx + b and added sliders for m and b then moved them so the students could see the effect. Here is the ready-made example available in Desmos:
They may not have made all the connection I want them to yet, but this plants the seed for the work we will do on Tuesday.
Wednesday 16 April 2014
MFM2P - Day 43
Day 43
Once a week the whole school stops what they are doing and reads for 30 minutes. Today West Reads fell during my grade 10 applied class so we read (most of us did anyway) for part of class.
We then continued with slope which we had really seen in terms of steepness yesterday. I emphasized that it is the ratio of the change in the dependent variable to the change in the independent variable, as opposed to talking about rise over run which many students seem to mix up. To explain why the ratio is not the other way around we looked at some examples and figured out what slope represented in each case. Here are a couple of those examples:
Next we talked about a slope of 0, an undefined slope along with positive and negative slope.
On to examples. We started with finding the slope of a graphed line.
Then we found the slope between two points without a graph. I like to have them focus on looking at the change in each variable separately. For the example below, I asked what the values of the y-variables were (some did not know), then "How do you get from -5 to -7?", "You go down 2", from which we get -2. Repeat for the change in x... "How do you get from -1 to 5?", "You go up 7", so +7. The slope is then the ratio of those numbers.
Students then started to work on a handout. We will need more time tomorrow to finish it up, but I think they understand the concept. I would like to tie this in with the equation of a line now, but you'll have to check back tomorrow to find out what I decided to do as I also feel the need to wrap up this cycle soon.
This was much more of a "lesson" than we usually do in this class. I could change that for next time, but I think it's okay to direct them a little more some of the time. I am happy that I can see how to tackle a topic differently. Teaching this course through spiraling or cycling is really helping me grow as a teacher.
Once a week the whole school stops what they are doing and reads for 30 minutes. Today West Reads fell during my grade 10 applied class so we read (most of us did anyway) for part of class.
We then continued with slope which we had really seen in terms of steepness yesterday. I emphasized that it is the ratio of the change in the dependent variable to the change in the independent variable, as opposed to talking about rise over run which many students seem to mix up. To explain why the ratio is not the other way around we looked at some examples and figured out what slope represented in each case. Here are a couple of those examples:
Next we talked about a slope of 0, an undefined slope along with positive and negative slope.
On to examples. We started with finding the slope of a graphed line.
Then we found the slope between two points without a graph. I like to have them focus on looking at the change in each variable separately. For the example below, I asked what the values of the y-variables were (some did not know), then "How do you get from -5 to -7?", "You go down 2", from which we get -2. Repeat for the change in x... "How do you get from -1 to 5?", "You go up 7", so +7. The slope is then the ratio of those numbers.
Students then started to work on a handout. We will need more time tomorrow to finish it up, but I think they understand the concept. I would like to tie this in with the equation of a line now, but you'll have to check back tomorrow to find out what I decided to do as I also feel the need to wrap up this cycle soon.
This was much more of a "lesson" than we usually do in this class. I could change that for next time, but I think it's okay to direct them a little more some of the time. I am happy that I can see how to tackle a topic differently. Teaching this course through spiraling or cycling is really helping me grow as a teacher.
Tuesday 15 April 2014
MFM2P - Day 42
Day 42
We started with elevator and bubble wrap estimations from Estimation 180, having skipped over the Christmas ones (despite the ridiculous snow today, it is not Christmas). I notice that my students' guesses are getting closer together - less crazy high and crazy low ones. They sometimes all underestimate or overestimate, which is interesting.
Next up: staircases from Fawn. I used this as an introduction to slope. You should read her post, really, go read it now, it's better than what I did! This activity was a great way of getting students talking about steepness and it was really interesting to see how they tried to measure it for #5. This image is from Fawn's blog:
As a class we looked at whether only the vertical height determined steepness or only the horizontal portion determined steepness (I provided diagrams as counter-examples). We agreed that both were important. I asked how we could get one number to represent steepness and, because I had an example with height and base width as well as step height and step width, one student related it to scale factor (which was awesome). I used to tie both to ratios. We settled on finding the ratio of height to base length which they did for the remaining examples and then we wrote our new order of least steep to most steep. I moved on to mentioning the word slope, but we did not get further than them gluing some slope pages in their comp books. We will continue this tomorrow.
We started with elevator and bubble wrap estimations from Estimation 180, having skipped over the Christmas ones (despite the ridiculous snow today, it is not Christmas). I notice that my students' guesses are getting closer together - less crazy high and crazy low ones. They sometimes all underestimate or overestimate, which is interesting.
Next up: staircases from Fawn. I used this as an introduction to slope. You should read her post, really, go read it now, it's better than what I did! This activity was a great way of getting students talking about steepness and it was really interesting to see how they tried to measure it for #5. This image is from Fawn's blog:
As a class we looked at whether only the vertical height determined steepness or only the horizontal portion determined steepness (I provided diagrams as counter-examples). We agreed that both were important. I asked how we could get one number to represent steepness and, because I had an example with height and base width as well as step height and step width, one student related it to scale factor (which was awesome). I used to tie both to ratios. We settled on finding the ratio of height to base length which they did for the remaining examples and then we wrote our new order of least steep to most steep. I moved on to mentioning the word slope, but we did not get further than them gluing some slope pages in their comp books. We will continue this tomorrow.
2048
I am fascinated by the game 2048. I have been playing it for a month or so now and it has not really lost its appeal. The fascinating thing is that it seems to appeal to so many people. Students play, whether they are in applied math or calculus or not taking math at all. Little kids play. Adults with varying skills and careers play. It has this mass appeal that seems fairly rare these days. I play less now that I have "conquered" the game, but there is always another level to reach. My best is 4096, but knowing that others have reached 8192 makes it a challenge.
Here is a quick explanation of how the game works. On a 4 by 4 grid you start with two tiles, both can be either a 2 or a 4. You can swipe right, left, up or down and it moves all the tiles in that direction and adds another tile. When you swipe, any two tiles next to each other with the same number will be combined. For example - given this:
Swiping left gives you this:
The goal is to get the 2048 tile (but you can keep going).
I have a degree in computer science so powers of 2 are somehow appealing to me. The simplicity of the game, the lack of time-pressure and the beauty of having that perfect chain to reach a new milestone are some of what makes it a game I like. But I also see the math in it. And wanted to take that a step further.
I collected some data and discovered that I am fairly consistent - it takes me about 12 minutes to "win". I recorded the length of time needed to get the first 8 tile, 16 tile, 32 tile, and so on up to 2048. If we consider 2 as the first tile then the 8 tile would be tile number 3, 16 would be tile number 4 and so on. I plotted the results in Desmos:
Nice! Exponential data that students can relate to (and gather themselves) that doesn't have to do with bacteria. But wait - how does the independent variable here (tile number) related to the number on the tile: 2, 4, 8, 16 ,32, etc.? It's the exponent in that sequence written as powers of 2. So we have used a log (base 2) scale to see our data this way. Cool! If you plot the time vs tile value you will see a linear relationship.
Although my school board has blocked the 2048 website, students can download a 2048 app or have their own data plan. I will be getting more data collection going in class and have them model this to find out how much time I need to set aside to reach 8192.
Update (May 17, 2014)
The folks at Desmos, being who they are, naturally replied to my tweet about this blog post.
Here is the cool stuff they did.
Here is a quick explanation of how the game works. On a 4 by 4 grid you start with two tiles, both can be either a 2 or a 4. You can swipe right, left, up or down and it moves all the tiles in that direction and adds another tile. When you swipe, any two tiles next to each other with the same number will be combined. For example - given this:
Swiping left gives you this:
The goal is to get the 2048 tile (but you can keep going).
I have a degree in computer science so powers of 2 are somehow appealing to me. The simplicity of the game, the lack of time-pressure and the beauty of having that perfect chain to reach a new milestone are some of what makes it a game I like. But I also see the math in it. And wanted to take that a step further.
I collected some data and discovered that I am fairly consistent - it takes me about 12 minutes to "win". I recorded the length of time needed to get the first 8 tile, 16 tile, 32 tile, and so on up to 2048. If we consider 2 as the first tile then the 8 tile would be tile number 3, 16 would be tile number 4 and so on. I plotted the results in Desmos:
Nice! Exponential data that students can relate to (and gather themselves) that doesn't have to do with bacteria. But wait - how does the independent variable here (tile number) related to the number on the tile: 2, 4, 8, 16 ,32, etc.? It's the exponent in that sequence written as powers of 2. So we have used a log (base 2) scale to see our data this way. Cool! If you plot the time vs tile value you will see a linear relationship.
Although my school board has blocked the 2048 website, students can download a 2048 app or have their own data plan. I will be getting more data collection going in class and have them model this to find out how much time I need to set aside to reach 8192.
Update (May 17, 2014)
The folks at Desmos, being who they are, naturally replied to my tweet about this blog post.
Here is the cool stuff they did.
Friday 11 April 2014
MFM2P - Day 41
Day 41
We jumped back into Estimation 180 today but they were hard! Ones like this (day 52):
were not met with much success. It is very difficult to gauge the thickness of the glass so my students were way off. This pattern continued for the next few estimations. I was surprised when one student had estimated 1212 ml (the highest guess of the class) for this one:
(The answer was 1210 ml.) She got a lollipop! We finished off with the turkey napkins question so that they would all feel better about their ability to estimate.
We moved on with surface area and volume. We worked through an example where they were given slant height but not vertical height.
They figured out that they needed to use the Pythagorean theorem in order to be able to calculate volume. Next, they worked on four problems involving surface area and volume of a pyramid. One required them to work backward to find the slant height and two had rectangular bases.
We finished up collecting some data which I will feature in a separate blog post.
We jumped back into Estimation 180 today but they were hard! Ones like this (day 52):
were not met with much success. It is very difficult to gauge the thickness of the glass so my students were way off. This pattern continued for the next few estimations. I was surprised when one student had estimated 1212 ml (the highest guess of the class) for this one:
(The answer was 1210 ml.) She got a lollipop! We finished off with the turkey napkins question so that they would all feel better about their ability to estimate.
We moved on with surface area and volume. We worked through an example where they were given slant height but not vertical height.
They figured out that they needed to use the Pythagorean theorem in order to be able to calculate volume. Next, they worked on four problems involving surface area and volume of a pyramid. One required them to work backward to find the slant height and two had rectangular bases.
We finished up collecting some data which I will feature in a separate blog post.
Thursday 10 April 2014
MFM2P - Day 40 Pyramids
Day 40
I decided that before jumping into surface area and volume of pyramids, I would get my students to build some pyramids. So I took in the bins of polydron manipulative pieces (I'm sure they have a proper name, but I don't know it) and put this on the board:
Play time! It was interesting to see some students struggling trying to make rectangles into pyramids. They figured out that the sides needed to be triangles and came up with lots of different pyramids.
One group also made a basket for all their pyramids:
Next we talked a little about vocabulary.
We then talked about how to find the surface area of a pyramid. I opened one up so they could see the net and they quickly told me (in their own words) that it is the sum of the area of the square and the area of the four triangles. I gave them a handout with all the information on it along with some examples for them to cut out and glue in their comp books. They did an example from the handout after we went over how to find the area of a triangle.
We then moved on to volume.
I gave them nets of right pyramids to cut out. Once folded they look like this:
If you put three of them together you can form a prism. I wish I had taken a picture of them (sorry!). It took the groups different lengths of time to get to this point so I walked around and had the same conversation with each group:
Me: "What shape did you create?"
S: "A prism." (some said a cube so we talked about how the height could be different from the side lengths of the base)
Me: "How can that help us figure out the volume of the pyramid?"
S: "We know how to calculate the volume of a prism."
Me: "How?"
S: "Length times width time height."
Me: "Okay, so what about the pyramid?"
S: "There are three of them so divide by 3?"
Having the prism made of pyramids in my hands was really helpful for showing students who had trouble grasping the relationship.
I thought this was pretty good use of the period so far. They got to do lots of hands-on stuff and hopefully understood how to find surface area and volume without relying on a formula sheet, which they so love to do. We finished up working through another example and will do one where they need to calculate slant height tomorrow.
In case you think my class is all sunshine and roses, it isn't. I found today extremely frustrating and waited several hours before blogging about what we did in order to calm down. However, I think this blog should be about what we are doing in class, not about "issues" that arise along the way that I have to deal with. I still think my students are fantastic, but today was not a good day for some...
I decided that before jumping into surface area and volume of pyramids, I would get my students to build some pyramids. So I took in the bins of polydron manipulative pieces (I'm sure they have a proper name, but I don't know it) and put this on the board:
Play time! It was interesting to see some students struggling trying to make rectangles into pyramids. They figured out that the sides needed to be triangles and came up with lots of different pyramids.
One group also made a basket for all their pyramids:
Next we talked a little about vocabulary.
We then moved on to volume.
I gave them nets of right pyramids to cut out. Once folded they look like this:
If you put three of them together you can form a prism. I wish I had taken a picture of them (sorry!). It took the groups different lengths of time to get to this point so I walked around and had the same conversation with each group:
Me: "What shape did you create?"
S: "A prism." (some said a cube so we talked about how the height could be different from the side lengths of the base)
Me: "How can that help us figure out the volume of the pyramid?"
S: "We know how to calculate the volume of a prism."
Me: "How?"
S: "Length times width time height."
Me: "Okay, so what about the pyramid?"
S: "There are three of them so divide by 3?"
Having the prism made of pyramids in my hands was really helpful for showing students who had trouble grasping the relationship.
I thought this was pretty good use of the period so far. They got to do lots of hands-on stuff and hopefully understood how to find surface area and volume without relying on a formula sheet, which they so love to do. We finished up working through another example and will do one where they need to calculate slant height tomorrow.
In case you think my class is all sunshine and roses, it isn't. I found today extremely frustrating and waited several hours before blogging about what we did in order to calm down. However, I think this blog should be about what we are doing in class, not about "issues" that arise along the way that I have to deal with. I still think my students are fantastic, but today was not a good day for some...
Wednesday 9 April 2014
MFM2P - Day 39
Day 39
As many students had not finished yesterday's task, they continued to work on that today. This is where I find things get tricky. I need to provide meaningful work to those who did finish the task that will not disadvantage those who won't do it today. We did surface area and volume of rectangular-based prism in the first cycle so I put together a handout with more of that and surface area and volume of triangular-based prisms. These were good because they tied together sum of squares (Pythagorean theorem) with surface area. Some finished all that and got to work on unit conversions (ugh). It was fine, but I need to come up with a better strategy for these kinds of days.
I thought we should end on a positive note so we did a couple of Estimation 180 questions which were fun.
As many students had not finished yesterday's task, they continued to work on that today. This is where I find things get tricky. I need to provide meaningful work to those who did finish the task that will not disadvantage those who won't do it today. We did surface area and volume of rectangular-based prism in the first cycle so I put together a handout with more of that and surface area and volume of triangular-based prisms. These were good because they tied together sum of squares (Pythagorean theorem) with surface area. Some finished all that and got to work on unit conversions (ugh). It was fine, but I need to come up with a better strategy for these kinds of days.
I thought we should end on a positive note so we did a couple of Estimation 180 questions which were fun.
Tuesday 8 April 2014
MFM2P - Day 38 Roof Truss
Day 38
Today was task day. They were allowed to use their notes to help them work through a task involving Pythagorean theorem, similar triangles and trig. The premise was that an architect was designing a cottage and the roof truss would like like the one pictured below. They were told that the king post needed to be at least 7' long and that the angle formed by the ridge beam and the rafter had to be between 15°and 45°.
They were then given data on king post length and corresponding rafter length for a constant ridge beam length and were asked to choose a truss design and calculate how much wood was needed for their design.
The immediate reaction was "I don't know what I'm supposed to do." and "This is stupid.". There was a lot of resistance to doing ANYTHING but we persevered (as in, I answered a LOT of questions to get them going) and they got to work. I suggested they start by finding the angle formed by the ridge beam and the rafter for each design. From there they chose a design and calculated all of the other lengths to figure out how much wood (length) would be needed for their design.
They also had to write about the connections between the mathematics involved and the construction of a roof truss.
Many students finished within the period, but some need more time. I also discovered that a few students had written very little and will need to continue tomorrow with some prompting. It's funny how some students will ask a bazillion questions and try to get reassurance for every step they take, while others will sit quietly and have no idea what to do next. I was answering questions for the entire period which is why I didn't notice these few students with very little work done. I will have to do a better job next time...
This task originally was designed for 2 days with the first day being spent exploring roof truss designs in groups with the help of Popsicle sticks and glue. Now I think my students are great but I didn't think that they would get a lot out of that exploration and I also thought that the mess they would create with the glue would not be fun to deal with. I was not up for that kind of "stickiness"! I am all for exploring a concept but I'm not sure that it would have helped them with the individual task. Maybe I'm wrong and maybe I'm not giving them enough credit for being able to explore and connect to the mathematics without getting off task.
Today was task day. They were allowed to use their notes to help them work through a task involving Pythagorean theorem, similar triangles and trig. The premise was that an architect was designing a cottage and the roof truss would like like the one pictured below. They were told that the king post needed to be at least 7' long and that the angle formed by the ridge beam and the rafter had to be between 15°and 45°.
They were then given data on king post length and corresponding rafter length for a constant ridge beam length and were asked to choose a truss design and calculate how much wood was needed for their design.
The immediate reaction was "I don't know what I'm supposed to do." and "This is stupid.". There was a lot of resistance to doing ANYTHING but we persevered (as in, I answered a LOT of questions to get them going) and they got to work. I suggested they start by finding the angle formed by the ridge beam and the rafter for each design. From there they chose a design and calculated all of the other lengths to figure out how much wood (length) would be needed for their design.
They also had to write about the connections between the mathematics involved and the construction of a roof truss.
Many students finished within the period, but some need more time. I also discovered that a few students had written very little and will need to continue tomorrow with some prompting. It's funny how some students will ask a bazillion questions and try to get reassurance for every step they take, while others will sit quietly and have no idea what to do next. I was answering questions for the entire period which is why I didn't notice these few students with very little work done. I will have to do a better job next time...
This task originally was designed for 2 days with the first day being spent exploring roof truss designs in groups with the help of Popsicle sticks and glue. Now I think my students are great but I didn't think that they would get a lot out of that exploration and I also thought that the mess they would create with the glue would not be fun to deal with. I was not up for that kind of "stickiness"! I am all for exploring a concept but I'm not sure that it would have helped them with the individual task. Maybe I'm wrong and maybe I'm not giving them enough credit for being able to explore and connect to the mathematics without getting off task.
Monday 7 April 2014
MFM2P - Day 37
Day 37
We jumped forward on Estimation 180 today. I decided it wasn't a good idea to estimate the number of blow pops with grade 10 boys in the room. Instead we looked at the height of a Ferris wheel, then estimated Fawn Nguyen's height and Nathan Kraft's height. Don't tell Fawn, but one student estimated her height (without the chair) at 4'6"!
Next we did a trig example together to refresh their memories. We found a side length given an angle and another side in a right triangle. They spent the next 10-ish minutes working on similar questions.
I have a confession. I have been avoiding making students work in new groups. I think this is because I didn't want to deal with the complaining that usually accompanies changing groups. However, I created a class for them on the on-line random group maker I have used in the past and pushed the button in front of them to create pairs for today's activity. As has been the case every time I have done this before, there were no complaints (what is wrong with me? why do I worry about this stuff???). They spent the remainder of the class working on stations. Each of six stations was posted on bright paper around the room and dealt with one topic that will be part of tomorrow's task. There was one for sum of squares (Pythagorean theorem), one for similar triangles, one for finding an angle using trig, and so on. Each group had an answer sheet which they had to show me after each station they completed. A correct answer earned them a sticker (I am constantly amazed at how much work they will do for stickers). I love doing stations as it gets them up and talking about math. The questions are no different than a worksheet, but students are much, much more engaged with stations. For a while anyway. They did start copying answers off each other after a while and there was more chatting going on and less math. I started having to ask to see work... One group did get through all the stations which was great.
We jumped forward on Estimation 180 today. I decided it wasn't a good idea to estimate the number of blow pops with grade 10 boys in the room. Instead we looked at the height of a Ferris wheel, then estimated Fawn Nguyen's height and Nathan Kraft's height. Don't tell Fawn, but one student estimated her height (without the chair) at 4'6"!
Next we did a trig example together to refresh their memories. We found a side length given an angle and another side in a right triangle. They spent the next 10-ish minutes working on similar questions.
I have a confession. I have been avoiding making students work in new groups. I think this is because I didn't want to deal with the complaining that usually accompanies changing groups. However, I created a class for them on the on-line random group maker I have used in the past and pushed the button in front of them to create pairs for today's activity. As has been the case every time I have done this before, there were no complaints (what is wrong with me? why do I worry about this stuff???). They spent the remainder of the class working on stations. Each of six stations was posted on bright paper around the room and dealt with one topic that will be part of tomorrow's task. There was one for sum of squares (Pythagorean theorem), one for similar triangles, one for finding an angle using trig, and so on. Each group had an answer sheet which they had to show me after each station they completed. A correct answer earned them a sticker (I am constantly amazed at how much work they will do for stickers). I love doing stations as it gets them up and talking about math. The questions are no different than a worksheet, but students are much, much more engaged with stations. For a while anyway. They did start copying answers off each other after a while and there was more chatting going on and less math. I started having to ask to see work... One group did get through all the stations which was great.
Friday 4 April 2014
MFM2P - Day 36
Day 36
When I walked into class a student asked "Are we doing estimation?" to which I replied "Do you want to?" and she said "Yes." so we did. We did days 33-37 today. I think I may start to jump around instead of doing them in order as some students are looking them up on their phone. Lollipops are a huge incentive! And that reminds me, I need to buy more.
We followed up the estimation with similar triangle work and then some trig. Many students were rusty on finding the measure of an angle in a right triangle given two sides. Hopefully they remember the process now. And that was it for today.
When I walked into class a student asked "Are we doing estimation?" to which I replied "Do you want to?" and she said "Yes." so we did. We did days 33-37 today. I think I may start to jump around instead of doing them in order as some students are looking them up on their phone. Lollipops are a huge incentive! And that reminds me, I need to buy more.
We followed up the estimation with similar triangle work and then some trig. Many students were rusty on finding the measure of an angle in a right triangle given two sides. Hopefully they remember the process now. And that was it for today.
Thursday 3 April 2014
MFM2P - Day 35
Day 35
We hit the toilet paper estimations today, some with video answers. This prompted one student to ask how [Mr. Stadel] had time to do this. I'm sure many of us have asked the same question!
The plan for today was to go outside to find the height of inaccessible objects using similar triangles. I thought we should go over how to solve for a missing side using similar triangles first, not least of which because I had a new student join my class at the beginning of cycle 2 who had therefore not seen similar triangles. So I handed out printouts of the great picture from the Estimation 180 site of Andrew and the lamppost and their shadows.
I wanted them to measure the two shadows and Andrew and use similar triangles to calculate the height of the lamppost on paper (I know they could just measure it, but they needed to practice using similar triangles). Then we would use Andrew's actual height to get the actual height of the lamppost. This did not go well. Picking up a ruler and measuring seemed a difficult task for some groups. Yes, they were doing this in groups - should have been straightforward, no? Apparently not. A couple of groups did find a scale factor around 3 but that is as far as they got. The other groups, well, they were still (or not) measuring. Sigh. This probably should have been an indication that taking these children outside to measure longer distances might not be a good idea...
However, I had said we would go outside so outside we went. The sun was not cooperating so we took the mirrors with us, along with measuring tapes and metre sticks. It was cold outside, but I had asked them to get their jackets. Getting them to do anything was painful. They really just wanted to break through the ice that had formed on puddles - as my 4-year old loves to do. Sigh. I got each group (I think) to get one set of measurements for the lamppost outside and then we went back in and I told them to figure out the height of the clock which is suspended from the ceiling. Again, a lot of non-activity followed. So I had to get them to stand up and walk over the to the clock and put their mirror on the ground and back up and ... Argh!
I think I tried to cram too much into today. I should have skipped the picture and gone straight to the two examples that were part of the handout for the actual activity. We should have practiced using the mirrors in class before venturing out. The funny thing is that I have done this activity many times before with kids who are less cooperative than the fantastic class I have this year, and it has gone really well. I think we will re-do it later in the semester when it warms up and add some clinometer action to the mix. In the meantime, I will pick up the pieces tomorrow.
We hit the toilet paper estimations today, some with video answers. This prompted one student to ask how [Mr. Stadel] had time to do this. I'm sure many of us have asked the same question!
The plan for today was to go outside to find the height of inaccessible objects using similar triangles. I thought we should go over how to solve for a missing side using similar triangles first, not least of which because I had a new student join my class at the beginning of cycle 2 who had therefore not seen similar triangles. So I handed out printouts of the great picture from the Estimation 180 site of Andrew and the lamppost and their shadows.
I wanted them to measure the two shadows and Andrew and use similar triangles to calculate the height of the lamppost on paper (I know they could just measure it, but they needed to practice using similar triangles). Then we would use Andrew's actual height to get the actual height of the lamppost. This did not go well. Picking up a ruler and measuring seemed a difficult task for some groups. Yes, they were doing this in groups - should have been straightforward, no? Apparently not. A couple of groups did find a scale factor around 3 but that is as far as they got. The other groups, well, they were still (or not) measuring. Sigh. This probably should have been an indication that taking these children outside to measure longer distances might not be a good idea...
However, I had said we would go outside so outside we went. The sun was not cooperating so we took the mirrors with us, along with measuring tapes and metre sticks. It was cold outside, but I had asked them to get their jackets. Getting them to do anything was painful. They really just wanted to break through the ice that had formed on puddles - as my 4-year old loves to do. Sigh. I got each group (I think) to get one set of measurements for the lamppost outside and then we went back in and I told them to figure out the height of the clock which is suspended from the ceiling. Again, a lot of non-activity followed. So I had to get them to stand up and walk over the to the clock and put their mirror on the ground and back up and ... Argh!
I think I tried to cram too much into today. I should have skipped the picture and gone straight to the two examples that were part of the handout for the actual activity. We should have practiced using the mirrors in class before venturing out. The funny thing is that I have done this activity many times before with kids who are less cooperative than the fantastic class I have this year, and it has gone really well. I think we will re-do it later in the semester when it warms up and add some clinometer action to the mix. In the meantime, I will pick up the pieces tomorrow.
Wednesday 2 April 2014
MFM2P - Day 34 Frogs!
Day 34
We started with more Estimation 180, at which they are getting very good. There were multiple correct answers for most of the estimations today (days 21-26). The range of answers is getting tighter too, except for Day 24 which asked "How many sheets of paper in the package?".
One student guessed 1000000. Yes, 1 million sheets. We talked about why this was a "too high" guess given that it meant that there would be over 83000 sheets in each pad of paper. I think they are starting to see that a combination of reasoning and calculations will help them get a good estimate.
Next, Frogs! This is a fun, yet challenging game.
I made them strips to work with and brought in square tiles to represent the frogs. Here is the sequence for 1 pair of frogs.
So 3 moves is the minimum. They recorded that in their table. Next, 2 pairs of frogs (feel free to play along):
This gave a minimum of 8 moves. Enter that in the table. Then on to 3 pairs:
I'll let you play with this and see what you find. I found it really helpful to have the strips as otherwise you can get lost as to which end has an empty spot. Most of my students found this challenging. Some needed help to get going and some needed me to show them (once) how to do the 3 pairs. They then had to be able to reproduce it. Not to spoil your fun, but the data here is quadratic again and once they found the pattern they entered their data in the graphing calculator to produce an equation. They were then able to answer the original question (10 pairs of frogs) using their equation.
Some finished this and another investigation into the number of diagonals in a polygon (also quadratic) before the end of the period, and others were still working through yesterday's activities. I love working with patterns and modelling so this is all right up my alley. I am so impressed with all they can do independently at this point in the course.
Tomorrow, inaccessible heights!
We started with more Estimation 180, at which they are getting very good. There were multiple correct answers for most of the estimations today (days 21-26). The range of answers is getting tighter too, except for Day 24 which asked "How many sheets of paper in the package?".
One student guessed 1000000. Yes, 1 million sheets. We talked about why this was a "too high" guess given that it meant that there would be over 83000 sheets in each pad of paper. I think they are starting to see that a combination of reasoning and calculations will help them get a good estimate.
Next, Frogs! This is a fun, yet challenging game.
I made them strips to work with and brought in square tiles to represent the frogs. Here is the sequence for 1 pair of frogs.
So 3 moves is the minimum. They recorded that in their table. Next, 2 pairs of frogs (feel free to play along):
This gave a minimum of 8 moves. Enter that in the table. Then on to 3 pairs:
I'll let you play with this and see what you find. I found it really helpful to have the strips as otherwise you can get lost as to which end has an empty spot. Most of my students found this challenging. Some needed help to get going and some needed me to show them (once) how to do the 3 pairs. They then had to be able to reproduce it. Not to spoil your fun, but the data here is quadratic again and once they found the pattern they entered their data in the graphing calculator to produce an equation. They were then able to answer the original question (10 pairs of frogs) using their equation.
Some finished this and another investigation into the number of diagonals in a polygon (also quadratic) before the end of the period, and others were still working through yesterday's activities. I love working with patterns and modelling so this is all right up my alley. I am so impressed with all they can do independently at this point in the course.
Tomorrow, inaccessible heights!
Subscribe to:
Posts (Atom)