After a great day at EdCampOttawa, I came home to a roast chicken dinner (yes, my husband is a great cook) along with roasted veggies. While helping himself to seconds, my 8-year old, Noah, complained that he hadn't gotten enough potatoes. My husband said that he had cut 4 potatoes into 4. The kids quickly figured out that there had been 16 potato slices. I then asked how many we would each get if they were equally distributed among us (us being 6 people). They tried 2 and counted up to 12, then tried 3 and counted up to 18 (in 3s) so they knew it was more than 2 but fewer than 3 pieces each. Noah then said that it wasn't 2 and a half. I asked him how he knew. He got mad at me, screamed that he wasn't doing this anymore and stomped away from the table. So I turned to Jacob, who is 6, and asked him the same question as I had seen him making gestures with his hands that looked like he was figuring it out. He told us that if they each got 2 and a half pieces, that would be 15 pieces. At some point my 10-year old said she had figured it out, but actually managed to not yell out the answer (good job, Isabelle!). So back to Jacob. We went back to knowing it was more than 2 pieces each which he told me would be 12 pieces. I asked how many pieces were left to be divided among us. He said 4. He wanted to give each kid 1 and the adults none, but I said we each had to get the same amount. Then he thought Noah shouldn't get any since he had left the table. With a little encouragement he said we could "chop, chop" the pieces into 3. So how many pieces would that make? 12, he counted. And then he figured that once around the table was 6 so he could around the table another time and we would each get 2 of the cut-up pieces. So 2 and two-thirds each. Just as we were saying this Noah yelled from the next room - 2 and a half and one sixth each! Yes, Noah. Yes :) Then he sat back down and finished eating.
Saturday 23 November 2013
Sunday 17 November 2013
Completing the Square with Algebra Tiles
There seems to be some interest in how to use algebra tiles in the MTBoS so I thought I would attempt a blog post. I apologize now if I confuse anyone - I don't claim to be an expert, but I do find they help kids make connections.
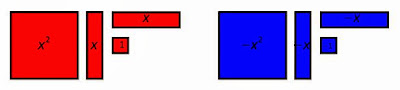
For years I avoided algebra tiles. It didn't help that one of my previous colleagues told the story of how one of her students managed to choke on a tile! Thankfully, none of my students have done that. Our tiles are red and blue so they all feel the need to look through them as if they are 3D glasses (sigh). The kids get to choose which should be positive and which should be negative. They invariably say red is hot so positive and blue is cold so negative so that is what I am using here.
We introduce the tiles in grade 9 when we simplify polynomials. They use them to multiply binomials (it makes a rectangle) and to factor trinomials (find the length and width of the rectangle). So my students are very familiar with algebra tiles by the time they get to completing the square.
I start with a warm-up to make sure they remember what is special about perfect square trinomials. They work in groups of 4 - each student does one question then they add up their answers. If the sum is correct, we can move on, if not, they have to find the error. I stole this from someone at TMC13 (who stole it from someone)^n, who stole it from Kate Nowak.
Students understand that instead of making a rectangle, they need to make a square with their tiles. They each have their own set to work with. We will place the 7 unit tiles off to the side and work with the rest.
They see that they need to add 1 unit tile to make a square. In order to do that we have to add a zero pair so a -1 unit tile goes with the 7 off to the side.
We can then write the area of the square a its side length squared and simplify the unit tiles. And just like that we have vertex form!
We work through a couple more examples in the same way, with students working with their tiles then consolidating with the whole class. Each time they have to divide the x-tiles - half for the length and half for the width so that they make a square. Each time they have to add unit tiles. I get them to notice patterns in what they are doing.
Next, we use a chart to connect the algebra tiles to the algebra. The cool thing is that they actually understand why we are dividing 'b' by 2 and squaring it because they have done it with the tiles.
The next day we extend to quadratics where 'a' is not equal to 1. Again we start with tiles and connect to algebra. You need identical tile diagrams for each x^2 you have, but it's the same process. It connects factoring out the 'a' value to the tiles.
I find algebra tiles really help explain why we are doing what we are doing. It helps that my students are asking how to change a quadratic from standard form to vertex form. Well, some of them are anyway!
My SMART Notebook file is here. I left off the extra practice for day 2 as I am not really happy with it, but am not sure how to change it.
If you are looking for on-line algebra tiles, The National Library of Virtual Manipulatives is a great resource.
For years I avoided algebra tiles. It didn't help that one of my previous colleagues told the story of how one of her students managed to choke on a tile! Thankfully, none of my students have done that. Our tiles are red and blue so they all feel the need to look through them as if they are 3D glasses (sigh). The kids get to choose which should be positive and which should be negative. They invariably say red is hot so positive and blue is cold so negative so that is what I am using here.
We introduce the tiles in grade 9 when we simplify polynomials. They use them to multiply binomials (it makes a rectangle) and to factor trinomials (find the length and width of the rectangle). So my students are very familiar with algebra tiles by the time they get to completing the square.
I start with a warm-up to make sure they remember what is special about perfect square trinomials. They work in groups of 4 - each student does one question then they add up their answers. If the sum is correct, we can move on, if not, they have to find the error. I stole this from someone at TMC13 (who stole it from someone)^n, who stole it from Kate Nowak.
Then we tackle our first example:
Students understand that instead of making a rectangle, they need to make a square with their tiles. They each have their own set to work with. We will place the 7 unit tiles off to the side and work with the rest.
They see that they need to add 1 unit tile to make a square. In order to do that we have to add a zero pair so a -1 unit tile goes with the 7 off to the side.
We can then write the area of the square a its side length squared and simplify the unit tiles. And just like that we have vertex form!
We work through a couple more examples in the same way, with students working with their tiles then consolidating with the whole class. Each time they have to divide the x-tiles - half for the length and half for the width so that they make a square. Each time they have to add unit tiles. I get them to notice patterns in what they are doing.
Next, we use a chart to connect the algebra tiles to the algebra. The cool thing is that they actually understand why we are dividing 'b' by 2 and squaring it because they have done it with the tiles.
The next day we extend to quadratics where 'a' is not equal to 1. Again we start with tiles and connect to algebra. You need identical tile diagrams for each x^2 you have, but it's the same process. It connects factoring out the 'a' value to the tiles.
I find algebra tiles really help explain why we are doing what we are doing. It helps that my students are asking how to change a quadratic from standard form to vertex form. Well, some of them are anyway!
My SMART Notebook file is here. I left off the extra practice for day 2 as I am not really happy with it, but am not sure how to change it.
If you are looking for on-line algebra tiles, The National Library of Virtual Manipulatives is a great resource.
Sunday 27 October 2013
Working with Integers
How many of us struggle with explaining integers? I know that I do. I find it most difficult to teach topics that are completely obvious to me, that I don't remember ever learning. So integers are right up there. Many years ago my friend, Tom Seidenberg, told me that he used the idea of a hot air balloon and sand bags. I ran with that and have been using it ever since. I am by no means saying that this is the best way to teach integers, but it does give students something concrete to hang on to. I must also say that my students have already been taught about integers, but many did not understand them the first time. This gives students a different way of thinking about integers. It takes a lot more than this to get them comfortable working with integers, but this is how I start.


Introducing Radian Measure
In our curriculum, students learn all about right angle trig and sine and cosine laws in grade 10. In grade 11 they learn about the graphs of trig functions, all done in degrees. In grade 12 they are introduced to radian measure. I was introduced to this by Tom Seidenberg, so I give full credit to him as this may be straight from their materials. I like the way it sets up what 1 radian is and gives a context to arc length over radius.
Link to Word document
Link to Word document
Quadratic Headbanz
My grade 10 academic math class is filled with great kids. For the last week or so we have been exploring quadratics in vertex and factored form, with the help of Desmos. My students are pretty solid at going between equations and their graphs. On Friday, about half of my class was away on a history field trip. We finished some questions from the previous day but I didn't want to start anything new - I wanted to do something fun! At TMC13, Sam Shah organized a Rational Headbanz game for the pre-calc group and I thought I could modify it for quadratics.
With the help of my colleague, Michelle, we made 30 headbanz. We used coloured card stock, cut into rectangles with 2 slits cut along the sides to accommodate ribbon. I wrote the equations and this is how they turned out:
The kids were pretty excited to play. I like to have written instructions on top of what I say, so here is what they saw:
They each got a whiteboard to record their work. It was interesting to see them thinking about what to ask. Many started with "Am I in vertex form?" or "Am I in factored form?" but the poor student who had had a hard time getting good answers. They had to think about what questions to ask. The nice thing is that those who were struggling heard the questions others were asking them and were able to move forward. The trickiest part was with the value of h in
had a hard time getting good answers. They had to think about what questions to ask. The nice thing is that those who were struggling heard the questions others were asking them and were able to move forward. The trickiest part was with the value of h in
They would ask "Is my h value positive?" but then either interpret the answer incorrectly or not be sure whether the person they had asked truly understood what a positive h value meant.
They all figured out their equations and had fun doing so. And they want to play again next week when the whole class is there. I'll be happy to oblige.
Thanks, Sam, for the inspiration : )
With the help of my colleague, Michelle, we made 30 headbanz. We used coloured card stock, cut into rectangles with 2 slits cut along the sides to accommodate ribbon. I wrote the equations and this is how they turned out:
The kids were pretty excited to play. I like to have written instructions on top of what I say, so here is what they saw:
They each got a whiteboard to record their work. It was interesting to see them thinking about what to ask. Many started with "Am I in vertex form?" or "Am I in factored form?" but the poor student who had
 had a hard time getting good answers. They had to think about what questions to ask. The nice thing is that those who were struggling heard the questions others were asking them and were able to move forward. The trickiest part was with the value of h in
had a hard time getting good answers. They had to think about what questions to ask. The nice thing is that those who were struggling heard the questions others were asking them and were able to move forward. The trickiest part was with the value of h in They would ask "Is my h value positive?" but then either interpret the answer incorrectly or not be sure whether the person they had asked truly understood what a positive h value meant.
They all figured out their equations and had fun doing so. And they want to play again next week when the whole class is there. I'll be happy to oblige.
Thanks, Sam, for the inspiration : )
Friday 27 September 2013
Back At It
I have been back at school for almost 4 weeks now. That looooong list of all the things that need to happen at the beginning of the year seems to be no less daunting after all these years that I have been teaching. As ever, it has felt like I've been running a race but the finish line keeps moving. The difference this year is that I seem to be the one (in part, anyway) who is moving that finish line. I have always wanted to do my best, but since becoming more active on Twitter, attending TMC13 and taking Jo Boaler's course, I feel like I have a better idea of how to improve. This means more work, of course, hence the unreachable finish line. And it has meant that I have not had time for Twitter which makes me feel disconnected from some of the people to whom I feel the most connected in this crazy math-teaching world : (
I want to attempt to briefly recap what I have been doing over the past 4 weeks in my 3 classes, but I will focus on my grade 9 academic class, as that is where most of my energy has been going.
I have 28 grade 9s (that's the maximum allowed here) and they are lovely. Really, they are all lovely kids. I let them sit where they wanted to and I learned their names on day 1. I told them that I wanted them to make mistakes, that making mistakes is how we learn. I told them we would be working on their number sense and on patterns. And we have. I have been doing counting circles with them, almost daily (thank you @wahedahbug!). It is not everyone's favourite thing, but we do it nonetheless. They all have to talk. They all see how to break up numbers and rearrange them. They see that when someone makes a mistake, it's not the end of the world, but that I turn it into a learning moment. I am making note of what we do for our counting circle each day - just flying by the seat of my pants, really. I noted that starting at 120 and going down by 3 was a poor choice as one student landed on 69 (sigh). I have done one math talk (12 x 15) with them, which I'm glad no one saw (to be improved upon next time). I introduced visual patterns from the start (the one shown below is a favourite of mine). Thank you @fawnpnguyen for creating this collection of patterns. We talked about a variable representing the generalization of a pattern. We saw the same pattern in many different ways - in terms of the picture and how to write it algebraically. We saw how to get from one algebraic representation to another. We did orangemallows when we talked about like terms. And we did "Like Term MATHO" (bingo). They worked in groups on big whiteboards. They did 5 quizzes which were all formative (all our quizzes are formative) upon which I only wrote feedback - no marks on anything. I also set up each quiz as half a page and repeated the questions on the bottom half of the page for them to show corrections. And it seems to be paying off as the results of their first test are better than they have been for a few years : )
I haven't felt the need to pour quite as much energy into my grade 10 class prep but am really enjoying brainstorming with my colleague after school each day. We talk about the next day's lesson and homework and tweak more than make big changes. Yesterday's class was all about finding the distance between two points which I introduce using Dan Meyer's Taco Cart 3-act. I have to explain to the kids that there are actually taco carts in California. No so many of those up here!
My grade 12 advanced functions class is a little on auto-pilot. We have used desmos a lot while exploring polynomial and rational functions. I love desmos. It helps students make connections and ask questions. All good. On Monday shared work problems will come up so I added the Bean Counting 3-act. We'll see how that goes.
And, only because I have so few pictures included in this post, here is one more. WCYDWT?
Tuesday 27 August 2013
Day -7
I start school in a week. (I'm going with the first day being day 0 since we have shortened classes and much mayhem.) Three of my own children started school today, leaving me home with only my 4-year old who will only go to school on Thursday this week (staggered start). As a result, I am trying to be productive and do some of what I had all summer to do, yet didn't.
Our grade 9 academic math course begins with polynomials and exponent laws. Ugh. Students struggle with this unit above all others and it is what we hit them with first. I had thought of changing the order but since taking Jo Boaler's "How to Learn Math" course, I think the problem lies in HOW we are teaching it. We need to work with patterns instead of having students simplify abstract expressions by remembering (or not) rules. What worked for many of us, does not work for so many of them. Attempting to work this in while keeping peace with my co-workers is challenging. We all teach the same thing on the same day using the same lesson. This can be a fantastic model if teachers are on the same page and truly working collaboratively...
I started by creating an activity sheet for kids to work through five linear patterns involving only positive quantities and five linear patterns that use positive and negative objects.
I stole most of these from Fawn Nguyen's Visual Patterns site. Thanks to Fawn's brilliant post on Pattern Posters for Algebra I, I have a better framework for what I am doing. I will start by working through a pattern with them (this is straight from Fawn - have I mentioned how much I love her?).
Or maybe two. You see, I am still not sure what I'm doing. By that I mean that not having done this particular activity in this course before, I'm not sure how it will play out. What patterns they will find. Whether they will differ from each other's and mine. What I will need to ask to get kids to persevere or get on the right track. How long it will take. I am fine with not knowing how it will go - I know where I want them to get and have a good idea of how to help them get there. However, I find it very difficult to just give this "lesson" to other teachers who may or may not buy in. I feel like I need some kind of narrative to go with it, but I don't have my own yet. Add to that the fact that the time will have to be "shared" with review from grade 8 (order of operations, working with fractions and integers) makes me feel overwhelmed. I would like to take the time to do this properly and I believe in doing that, the review will happen naturally. But I know that will not fly with some of my colleagues so I have to try to make it all work together. And I need to have this sorted out by tomorrow (!) as others need to photocopy. So any advice you can give would be great!
Our grade 9 academic math course begins with polynomials and exponent laws. Ugh. Students struggle with this unit above all others and it is what we hit them with first. I had thought of changing the order but since taking Jo Boaler's "How to Learn Math" course, I think the problem lies in HOW we are teaching it. We need to work with patterns instead of having students simplify abstract expressions by remembering (or not) rules. What worked for many of us, does not work for so many of them. Attempting to work this in while keeping peace with my co-workers is challenging. We all teach the same thing on the same day using the same lesson. This can be a fantastic model if teachers are on the same page and truly working collaboratively...
I started by creating an activity sheet for kids to work through five linear patterns involving only positive quantities and five linear patterns that use positive and negative objects.
I stole most of these from Fawn Nguyen's Visual Patterns site. Thanks to Fawn's brilliant post on Pattern Posters for Algebra I, I have a better framework for what I am doing. I will start by working through a pattern with them (this is straight from Fawn - have I mentioned how much I love her?).
Or maybe two. You see, I am still not sure what I'm doing. By that I mean that not having done this particular activity in this course before, I'm not sure how it will play out. What patterns they will find. Whether they will differ from each other's and mine. What I will need to ask to get kids to persevere or get on the right track. How long it will take. I am fine with not knowing how it will go - I know where I want them to get and have a good idea of how to help them get there. However, I find it very difficult to just give this "lesson" to other teachers who may or may not buy in. I feel like I need some kind of narrative to go with it, but I don't have my own yet. Add to that the fact that the time will have to be "shared" with review from grade 8 (order of operations, working with fractions and integers) makes me feel overwhelmed. I would like to take the time to do this properly and I believe in doing that, the review will happen naturally. But I know that will not fly with some of my colleagues so I have to try to make it all work together. And I need to have this sorted out by tomorrow (!) as others need to photocopy. So any advice you can give would be great!
Thursday 1 August 2013
It's Not Easy Being Us
Being a connected educator is hard! It takes time and dedication and time and organization and time and willingness to learn and share and time. Attempting to stay on top of twitter feeds and blog posts is nearly impossible while teaching full time and having some kind of life outside school. However, it is, for me, the only way to be a teacher. I want to learn and get better at what I do. I love to teach. I love to see that spark in the kids' eyes when they "get it". I love seeing the satisfaction a kid feels when they have struggled through a problem and finally understand. I love seeing kids have fun in class and hearing them talk about it afterwards. I love having a positive influence on their lives. But I know I don't always. I know I have done things "the wrong way" a lot. Which is why the MTBoS is so important to me. I want to continue improving. Had I not been deeply into Twitter I would not have known about Twitter Math Camp, which is the most valuable PD I have ever had. I would not have known about Jo Boaler's "How to Learn Math" course from which I have learned a tremendous amount. I would not have found all those 3-act math tasks, great ideas from Fawn or my favourite classroom game from Nathan. I would not have heard about so many great teaching books that will help me continue to learn more and get better. I would not have been exposed to people who think differently than I do and make me think deeply.
None of this could have happened for me if I hadn't committed to Twitter. It is akin to a relationship in that if you don't invest any time in it, you aren't really going to get much out of it. There are times when I cannot get on Twitter. Days may go by when I am swamped with school stuff and kid stuff and just have to let it go. But Feedly keeps on collecting blog posts for me to read so that I hopefully won't miss anything great. And the great thing about Twitter is that you can just jump right back in.
My colleagues at school, like many of yours, brush off any mention of Twitter. They don't understand its value. They say they don't have time. I make time. My kids are into Jiu-Jitsu so I am at the dojo five days a week. I mark tests there. I catch up on Twitter there. I read blog posts there. I write blog posts there. I get to school very early every day to get work done. My life is such that I have to be efficient with my time. My house may not be clean (ever) but my children are (mostly) happy, always well fed :) and loved and my students always get the best I can give. Being the best I can be is a moving target though - there's always something else that comes along to challenge me. And I accept that challenge!
In the title I wrote that it's not easy being "us". I really believe that despite geographic separation, we, the MTBoS, are connected in our love for learning and becoming better teachers. We support each other and genuinely care. What more could I ask for?
Monday 29 July 2013
TMC13 - Minus the Math
Twitter Math Camp 2013 ended yesterday. It was an incredible experience - 4 days with strangers-turned-friends all centered around teaching math. Perhaps not everyone's idea of a good time, but my idea of heaven! There were so many great teaching ideas presented and there are bound to be recaps of those (Greg Taylor @mathtans did a fantastic job while at TMC - I don't think he slept!) so I'm going to take a different tack.
The biggest point I want to make for anyone who wasn't at TMC13 is how inclusive it is. I have never been around a more welcoming, non-judgmental group of (awesome) people. I went there kinda-sorta knowing one person and made all kinds of friends! I am a quiet and shy person and discovered a number of people like me (who knew?!?) and lots of people who seemed okay with hanging out with me, despite my lack of outgo-i-ness (yes, I just made that word up). Not to say that there weren't times that I was feeling oh-so intimidated. The most awesome of which was dinner with David Wees (@davidwees) , Christopher Danielson (@Trianglemacsd), Eli Luberoff (@eluberoff/@desmos) and Sadie Estrella (@wahedahbug). As if that wasn't enough, we were joined by much of team Mathalicious - Karim Ani (@karimkai), Matt Lane (@mmmaaattttttt), Ginny Stuckey (@gstuck) and later by Chris Lusto (@lustomatic) and his girlfriend. Ever know that you are, without a doubt, the least smart person around a table? Yeah... But the food was delicious and I listened to a lot of great conversations. My point is that I never had to eat alone or miss going out - I just went to the hotel lobby and (quietly) joined in with whatever people were doing - sitting around talking, origami, getting tied up in knots... I realize that some of you may not realize what a HUGE deal that is, but it is. So, thank you to everyone at TMC13 for that.
Okay... here are a few fun non-math facts I learned at TMC13:
- Connie H. is not an axe-murderer (important in a roommate you have never met! Thanks, Connie!)
- Max is one of the most genuine and nice people around
- Nathan really is crazy. He was just "that crazy toothpick guy" before.
- Jami is not a ... (or dumb, apparently)
- Glenn can't remember names (but that makes retelling of stories a lot of fun)
- Sadie has a potty mouth
- Sam loves sparkles
- Eli managed to make everyone have a math crush on him by showing off Desmos (how weird does that make us?!?)
- Ashli is the folding queen
- Julie really is that positive and excited about everything!
- Elizabeth loves Flakes
- Don't be late for Lisa's class
I need to remember the following for next year:
- Actually talk to people whom I find intimidating (Fawn, Nathan, Karim...)
- Take pictures. Maybe even with me in them (that's just crazy talk now).
- Find something worthy of sharing. And share it (more crazy talk).
I also love that I now read tweets and blog posts in the voice of the author.
Thank you so much to Lisa and the TMC13 Team for all of their time and effort putting together the best conference any math teacher could ask for. <3
The biggest point I want to make for anyone who wasn't at TMC13 is how inclusive it is. I have never been around a more welcoming, non-judgmental group of (awesome) people. I went there kinda-sorta knowing one person and made all kinds of friends! I am a quiet and shy person and discovered a number of people like me (who knew?!?) and lots of people who seemed okay with hanging out with me, despite my lack of outgo-i-ness (yes, I just made that word up). Not to say that there weren't times that I was feeling oh-so intimidated. The most awesome of which was dinner with David Wees (@davidwees) , Christopher Danielson (@Trianglemacsd), Eli Luberoff (@eluberoff/@desmos) and Sadie Estrella (@wahedahbug). As if that wasn't enough, we were joined by much of team Mathalicious - Karim Ani (@karimkai), Matt Lane (@mmmaaattttttt), Ginny Stuckey (@gstuck) and later by Chris Lusto (@lustomatic) and his girlfriend. Ever know that you are, without a doubt, the least smart person around a table? Yeah... But the food was delicious and I listened to a lot of great conversations. My point is that I never had to eat alone or miss going out - I just went to the hotel lobby and (quietly) joined in with whatever people were doing - sitting around talking, origami, getting tied up in knots... I realize that some of you may not realize what a HUGE deal that is, but it is. So, thank you to everyone at TMC13 for that.
Okay... here are a few fun non-math facts I learned at TMC13:
- Connie H. is not an axe-murderer (important in a roommate you have never met! Thanks, Connie!)
- Max is one of the most genuine and nice people around
- Nathan really is crazy. He was just "that crazy toothpick guy" before.
- Jami is not a ... (or dumb, apparently)
- Glenn can't remember names (but that makes retelling of stories a lot of fun)
- Sadie has a potty mouth
- Sam loves sparkles
- Eli managed to make everyone have a math crush on him by showing off Desmos (how weird does that make us?!?)
- Ashli is the folding queen
- Julie really is that positive and excited about everything!
- Elizabeth loves Flakes
- Don't be late for Lisa's class
I need to remember the following for next year:
- Actually talk to people whom I find intimidating (Fawn, Nathan, Karim...)
- Take pictures. Maybe even with me in them (that's just crazy talk now).
- Find something worthy of sharing. And share it (more crazy talk).
I also love that I now read tweets and blog posts in the voice of the author.
Thank you so much to Lisa and the TMC13 Team for all of their time and effort putting together the best conference any math teacher could ask for. <3
Friday 14 June 2013
Meet her Where she Is
A recent event outside of school has prompted me to think about what I do in school with students who are lacking some of the basic skills needed to be successful in a particular math course. To begin, I need to talk about Chloë.
Sunfish, class 1. There are 3 students in the class but the other 2 girls are quite a bit older than Chloë and have both done Sunfish (quite successfully) at least once. Seeing the other girls meeting all the expectations for the end of this level on the first day completely intimidated my little 3-year old. She shut down, didn't want to try (because she knew she couldn't do an unassisted back float for 5 seconds as the other girls were) and looked so very, very sad. <insert my heart breaking here>
Sunfish, class 2. Only 2 students this time, but Chloë was still being asked to do things she knew she couldn't. And she wasn't getting the help she needed to learn or the support and encouragement she desperately needed to have the confidence in herself to try. At the end of that class her coach came to talk to me, basically to tell me that she was in the wrong level. I did my best to remain polite while I told her that Chloë was in the right level but that she should not be expected to do what the others in the class were already doing. The coach needed to meet her where she was and build on that foundation. (it turns out that the coach did not know what the expectations coming out of Salamander were - argh!)
The parallel to grade 9 math is clear to me. These students come to our school from a number of feeder schools, all having learned the same curriculum but in different ways and to different degrees. Some can't multiply without a calculator, some have had teachers who don't like math and therefore did as little of it as possible, while others have done all kinds of problem solving and learned far beyond the grade 8 curriculum. It is up to me to meet them where they are. To figure out what they know and where they need help. It is not for me to say that they are in the wrong level 3 weeks into my class (we have academic and applied grade 9 math).
My goal for next year is to do this better. Not just at the beginning of the semester, but throughout. I like a lot of what I have read about SBG and will implement that in my own way next year. At my school, quizzes are all formative. For each unit, there is a test and a task that count. Students can rewrite one unit test at the end of the semester. My plan is to use levels (R,1,2,3,4) to assess all quizzes and any students who do not achieve at least a level 3 will have to take that quiz again until they do. Each quiz will likely cover one or two specific curriculum expectations. My hope is that by ensuring that students have a solid understanding of all the pieces of the unit, they will be better able to put it all together for the test and task. This will require organization on my part (but I'm good with that) and work over the summer developing all the quizzes. This should be worth the extra work as I hope that it will help me better support my students where they are and lead them to where they need to be.
P.S. Sunfish, class 3 was better! The coach heard what I said and Chloë had a much better class : )
P.S. Sunfish, class 3 was better! The coach heard what I said and Chloë had a much better class : )
Friday 31 May 2013
Boat on the River
Catching up - Part II
We were about to start right-angle trig and I didn't want to just tell them the ratios without any reason for all of this. Naturally, I went over to Andrew Stadel's 3-Act Catalog and came upon Boat on the River. It was perfect!
Here is the video for Act I. Go on, watch it. It only takes 12 seconds. So cool! There were lots of questions flying around the room, then we got down to one:
We talked about the word "trigonometry" and how trig is used (Canadarm2 on ISS) and then looked at the ratio of sides of similar triangles (they each created their own triangle, similar to mine).
 We talked about how one of the ratios represents the slope and how it changes as you change the angle but that it does not change if you scale up/down the side lengths.
We talked about how one of the ratios represents the slope and how it changes as you change the angle but that it does not change if you scale up/down the side lengths.
I made a trig table for tangent, but called the columns "angle" and "slope" so they could find the angle that corresponds to any slope. Then I told them that the slope ratio has another name: tangent. We looked at some examples from the table and talked about that magical 45 degree angle.

After going over sine and cosine and working through a number of examples it was time for act II. They quickly came up with what we needed to know:
And that's what they got. Sort of. Many of them laughed when they saw 6". "That's not 6 inches!".

They didn't notice the bottom left corner:

This leads nicely to another good conversation about similar triangles.
They worked out the angle proudly using their new knowledge...
And then we got to see if the captain had done the math before attempting to go under the bridge - Act III. The video is here (54 seconds - with just the right music too).
This gave what we needed to do purpose. It engaged them and they HAD to see whether the boat made it. Another huge thank you to Mr. Stadel - you rock!
We were about to start right-angle trig and I didn't want to just tell them the ratios without any reason for all of this. Naturally, I went over to Andrew Stadel's 3-Act Catalog and came upon Boat on the River. It was perfect!
Here is the video for Act I. Go on, watch it. It only takes 12 seconds. So cool! There were lots of questions flying around the room, then we got down to one:
We talked about the word "trigonometry" and how trig is used (Canadarm2 on ISS) and then looked at the ratio of sides of similar triangles (they each created their own triangle, similar to mine).
 We talked about how one of the ratios represents the slope and how it changes as you change the angle but that it does not change if you scale up/down the side lengths.
We talked about how one of the ratios represents the slope and how it changes as you change the angle but that it does not change if you scale up/down the side lengths. I made a trig table for tangent, but called the columns "angle" and "slope" so they could find the angle that corresponds to any slope. Then I told them that the slope ratio has another name: tangent. We looked at some examples from the table and talked about that magical 45 degree angle.

After going over sine and cosine and working through a number of examples it was time for act II. They quickly came up with what we needed to know:
And that's what they got. Sort of. Many of them laughed when they saw 6". "That's not 6 inches!".

They didn't notice the bottom left corner:

This leads nicely to another good conversation about similar triangles.
They worked out the angle proudly using their new knowledge...
And then we got to see if the captain had done the math before attempting to go under the bridge - Act III. The video is here (54 seconds - with just the right music too).
This gave what we needed to do purpose. It engaged them and they HAD to see whether the boat made it. Another huge thank you to Mr. Stadel - you rock!
Wednesday 29 May 2013
Maximizing Area of a Rectangle
Catching Up - Part I
You know how it is. We are approaching the end of the year and there is so much to do. And somehow blogging takes a back seat, even though I know that I need to do it right away or I lose some of the detail. Thankfully I take pictures so I can remember what I was going to blog about!
Last week we were looking at the dimensions that will produce the rectangle with maximum area given a fixed perimeter. Everyone has probably taught this at some point and I don't think that I'm doing anything particularly exciting but I am trying to put more of the learning in the kids' hands and do less "telling". So, this is how I started:
They each had their own perimeter but they worked together. They had Cuisenaire rods to build the different sized rectangles. (As an aside, I would really have liked them to have had something flexible (pipe cleaners? to be able to make the rectangles as some didn't understand what I was talking about.)
This is what they came up with:
It was interesting to see that most chose even numbers. There were lots of multiples of 4 which worked out nicely, but it was great to talk about the options for the perimeters which were not multiples of 4 and especially to talk about the one odd perimeter.
Task 2 took a little longer for them to figure out and again, so many even numbers!
We went through what they came up with and then worked out the whole number possibilities for a perimeter of 20.
Then we generalized - they seemed to feel good about being able to answer the question for some ridiculously large perimeter.
You know how it is. We are approaching the end of the year and there is so much to do. And somehow blogging takes a back seat, even though I know that I need to do it right away or I lose some of the detail. Thankfully I take pictures so I can remember what I was going to blog about!
Last week we were looking at the dimensions that will produce the rectangle with maximum area given a fixed perimeter. Everyone has probably taught this at some point and I don't think that I'm doing anything particularly exciting but I am trying to put more of the learning in the kids' hands and do less "telling". So, this is how I started:
They each had their own perimeter but they worked together. They had Cuisenaire rods to build the different sized rectangles. (As an aside, I would really have liked them to have had something flexible (pipe cleaners? to be able to make the rectangles as some didn't understand what I was talking about.)
This is what they came up with:
It was interesting to see that most chose even numbers. There were lots of multiples of 4 which worked out nicely, but it was great to talk about the options for the perimeters which were not multiples of 4 and especially to talk about the one odd perimeter.
Task 2 took a little longer for them to figure out and again, so many even numbers!
We went through what they came up with and then worked out the whole number possibilities for a perimeter of 20.
Then we generalized - they seemed to feel good about being able to answer the question for some ridiculously large perimeter.
Friday 17 May 2013
Fawn vs. Nathan
I had my grade 9 class work on this problem today:
A colleague gave me a version of this that was fully scaffolded, but I thought it would be much richer if it was more open. And I threw a couple of tweep's names in there for fun.
They worked in groups and wrote solutions on their whiteboards. Here was the first attempt:

Although Fawn probably likes this, I asked if volume should determine the price. A. said "Surface area!" and this is what he produced:
And another solution:
Along the way I heard a lot of "Fawn's right!" and some "Nathan's wrong!" (maybe I should have won your little exponent game, Nathan)
They worked out that the volume of the large fish tank was 8 times the volume of the small one. The surface area of the large one was 4 times the surface area of the small one. The price of the large one was 4.6 times the price of the small one. Here is a nice summary (she originally forgot that there was no top so had to subtract after):
Bottom line here - Fawn is right! (always, otherwise she punches you)
A colleague gave me a version of this that was fully scaffolded, but I thought it would be much richer if it was more open. And I threw a couple of tweep's names in there for fun.
They worked in groups and wrote solutions on their whiteboards. Here was the first attempt:

Although Fawn probably likes this, I asked if volume should determine the price. A. said "Surface area!" and this is what he produced:
And another solution:
Along the way I heard a lot of "Fawn's right!" and some "Nathan's wrong!" (maybe I should have won your little exponent game, Nathan)
They worked out that the volume of the large fish tank was 8 times the volume of the small one. The surface area of the large one was 4 times the surface area of the small one. The price of the large one was 4.6 times the price of the small one. Here is a nice summary (she originally forgot that there was no top so had to subtract after):
Bottom line here - Fawn is right! (always, otherwise she punches you)
Similar Triangles
Today we started the unit on trigonometry. We begin with similar triangles so I came up with this investigation - what makes two figures similar? Students worked in groups of three, armed with rulers and protractor in order to measure the side lengths and angles of three sets of similar figures. As a group they had to write down the properties of similar figures on their whiteboards.
They quickly determined that the angles all had to be equal, but didn't see the relationship between the sides. I found that I had to ask a lot of questions to get them thinking about those side lengths.
me: "Which sides should you compare?"
student: "The two longest."
me: "Can you tell which sides to compare without knowing all the lengths?"
student: "No. Yes... Angles!"
me: "Okay, so now compare them."
The shapes I created were interesting in that several sides on the larger shape appeared to be 1 cm longer than the corresponding sides on the smaller shape. They were sure they had the right answer until I pointed out the side where that didn't work. One group even calculated the differences between corresponding sides:

They could see that increasing/decreasing by a fixed amount was not the right strategy. It was very interesting to see who came up with the idea of trying to find a number to multiply each of the smaller sides by to get the larger sides. They erased and calculated the ratio of corresponding side lengths and voilà! Scale factor!
 That was followed up with the second side of the sheet to solidify what they had figured out.
That was followed up with the second side of the sheet to solidify what they had figured out.
This activity was simple yet pushed some of them to think when they thought they already knew the answer. They needed to be able to explain their reasoning to each other and to me.
Whether they remember any of it on Tuesday remains to be seen!
They quickly determined that the angles all had to be equal, but didn't see the relationship between the sides. I found that I had to ask a lot of questions to get them thinking about those side lengths.
me: "Which sides should you compare?"
student: "The two longest."
me: "Can you tell which sides to compare without knowing all the lengths?"
student: "No. Yes... Angles!"
me: "Okay, so now compare them."
The shapes I created were interesting in that several sides on the larger shape appeared to be 1 cm longer than the corresponding sides on the smaller shape. They were sure they had the right answer until I pointed out the side where that didn't work. One group even calculated the differences between corresponding sides:

 That was followed up with the second side of the sheet to solidify what they had figured out.
That was followed up with the second side of the sheet to solidify what they had figured out. This activity was simple yet pushed some of them to think when they thought they already knew the answer. They needed to be able to explain their reasoning to each other and to me.
Whether they remember any of it on Tuesday remains to be seen!
Thursday 16 May 2013
Fractions are not Frightening
At supper tonight, Isabelle told her little brother, Jacob, that he is 12 halves. He had no idea what she was taking about. She proceeded to explain to him that she could take 6 and write it in terms of halves by doubling 6 and getting 12. He was not impressed. But he's 6 and there was no Star Wars Lego involved so this is not surprising.
I couldn't let this opportunity pass so I asked Isabelle if she knew that she is 125 twelfths. She looked at me with a confused-yet-I-accept-this-challenge look and started thinking it through. Then she gave up and asked for the answer. Fat chance! I asked her how many months there are in a year. Light bulb...she got the 120 twelfths and thought she had finished. I asked her what month we are. Another light bulb...only this was was not shining as brightly! She came up with 120 twelfths and 1/5 (it has been 5 months since her birthday). Nope. And no to giving her the answer. She wanted paper. Nope (we were eating) - I told her she had all the pieces already. And she thought about it a little more and got 10 and 5/12 which is 120/12 and 5/12 or 125/12.
Then we said that Noah is 101/12, but she was done (and apparently no one cared how old Chloë is, but she was refusing to eat her supper, so I guess that's fair.) That's okay - fractions are such a mystery to so many kids, I am glad that mine think they are kind of fun. Hmmm....this is probably exactly what my students think I do at home!
I couldn't let this opportunity pass so I asked Isabelle if she knew that she is 125 twelfths. She looked at me with a confused-yet-I-accept-this-challenge look and started thinking it through. Then she gave up and asked for the answer. Fat chance! I asked her how many months there are in a year. Light bulb...she got the 120 twelfths and thought she had finished. I asked her what month we are. Another light bulb...only this was was not shining as brightly! She came up with 120 twelfths and 1/5 (it has been 5 months since her birthday). Nope. And no to giving her the answer. She wanted paper. Nope (we were eating) - I told her she had all the pieces already. And she thought about it a little more and got 10 and 5/12 which is 120/12 and 5/12 or 125/12.
Then we said that Noah is 101/12, but she was done (and apparently no one cared how old Chloë is, but she was refusing to eat her supper, so I guess that's fair.) That's okay - fractions are such a mystery to so many kids, I am glad that mine think they are kind of fun. Hmmm....this is probably exactly what my students think I do at home!
Saturday 11 May 2013
The Week All Squared Away
Friday. Last period of the day. My energetic and lovely
grade 9s. And the topic of the day is the Pythagorean theorem, which they
have done in grades 7 and 8, so it's not always, uh, exciting, shall we
say. However, the majority of students only seem to remember "a
squared plus b squared equals c squared" as if every right triangle would
be labelled with a, b and c, the latter being the hypotenuse. (I have been know
to quickly draw a triangle labelled with a, b and c where a is the hypotenuse -
that confuses them.) So today I decided to do part of an activity that I
stole from Alex Overwijk (26 Squares), World Freehand Circle Drawing
Champion. (That is another story which you can also read on his blog... it all started when
we taught together many years ago, but being somewhat shorter than Alex, I was
not part of any of it!)
Back to today. Students walked in to find these
instructions:
Each group received a package with squares of side length 1 to 26. With four students per group, it did not take long to cut them out. I also provided them with an envelope in which to place the squares as they cut them out. Still M. managed to lose to the 2 square. Sigh... Then they got to play but quickly converged on creating a triangle with the sides of the squares. Perfect. Next question:
I gave each group a whiteboard and let them argue about who was right. "Of course you can make a triangle with any 3 squares!" "No, you can't - try with 1, 2 and 26." Z tries... "Well, that's just a fluke." FYI - by fluke he meant "I was wrong." I prompted some groups to think about if they made the smaller squares progressively larger, at what point would it actually form a triangle. This took the form of "What if that 3 was a 4? Keep going with that." They came up with the limiting case when the sum of the two smaller sides equaled the longer side and wrote it like this:
Off to work they went, trying out lots of
possibilities. My instructions we clearly not adequate for this part as
they came up with combinations that looked like they could be right triangles,
but in fact, were not. We talked about this, and next time I would have
them place the three triangles on the grid side of their whiteboards to ensure
that they truly had a 90 degree angle. If time allowed I would also get
them to go back and check their work after we established what makes this
"work".
We talked about a combination that worked (3, 4, 5) and I asked why they thought we were using squares, not just strips of length 1 to 26. We talked about area.
We consolidated by listing combinations that worked and
they noticed a pattern between:
so we came up with more! I also eventually showed them a list of Pythagorean triples on-line. One of them said "But there would be an infinite number of them, right?". : )
The time flew by - gotta love a Friday afternoon when
they aren't all looking at the clock!
Subscribe to:
Posts (Atom)