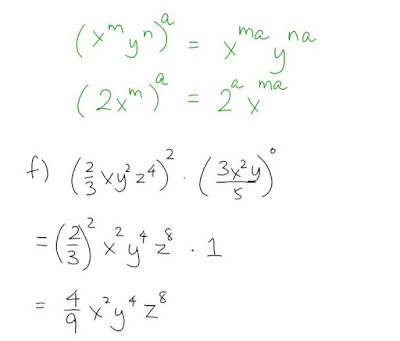Last Wednesday was a heartbreaking day for my family. Willow, our Bernese Mountain Dog, died. She was only four years old and losing her has been harder than any of our previous dogs. She had had emergency surgery on the Sunday and the vet said all went well. But she didn't get better.
We first met her and the other seven balls of fluff from her litter when they were only five weeks old. She came home at eight weeks and met Harmonie who taught her many of the things dogs need to know. She was full of mischief and such a lap dog, despite being 85 lbs. She loved big piles of leaves and snow and canoe rides (swimming is greatly overrated) and most of all her soccer ball (after she got rid of all of its stuffing). After we lost Harmonie a couple of years ago she grabbed all the attention from all of her people. She always hopped up on the couch to wait for me when I put the kettle on to make tea as she knew that it was almost cuddle time. She was a good dog.
Rest in peace, Willow.
There has been lots of buzz on Twitter around Name Tents (Feedback Forms) and rightfully so. I love using them and wrote about the tweaks I made to Sara Van Der Werf's template last year here. This included adding a picture of each student and finding out about their siblings. I have since started asking for pronouns, though I tell the class that this is optional as I do not want anyone to feel uncomfortable with what they share. I learn a lot about my students and they get to know me a little along the way.
At this time a year ago I felt really strongly that I wanted to keep these conversations going throughout the semester. I needed to work harder at fostering a positive relationship with all of my students so I created "Just Checking In..." sheets. I gave my first one at the end of the second week of school. Here is what it looked like:
This gave students an avenue to tell me if things weren't going well or if everything was just fine. It gave me a way to start a new conversation and to connect with all my students.
I continued checking in every few weeks. Here are some samples of questions/prompts.
If you haven't jumped on the "Two Nice Things" bandwagon yet, read more from Elissa Miller here.
I never required students to complete these, but they did. And at the end of June last year I had a student write me a thank you card that included "I loved when you asked us how we are doing. No other teacher has done that and it made me feel very good." Sometimes it's the little things we do that have a large impact.
I wanted to do something a little different with my grade 9 class as they prepare for EQAO and their final exam. My plan was to focus on equations of lines so I made some "Add Them Up" questions. I formed random groups of four students by having them draw playing cards and each group received the same sheet. On it were four different versions of the same question. Each group member worked on one question (they took small whiteboards for this) and when they all finished, the sum of their answers was written in the centre. This makes checking answers easy for me and forces the group to find mistakes if the sum is incorrect. Here is the first one:
I made five of these, with the level of difficulty increasing each time. Here is the last one:
I photocopied these on five different colours of paper so that I could easily tell which one each group was working on. I was surprised by the number of mistakes, though many came up when they had to add fractions to get the sum of their answers. Fractions are hard. I purposely made many of the answers fractions so that they would be forced to practice these skills. As it turns out, some were really "ugly" so I have edited them and they are now more reasonable.
I was really impressed with my class - they helped each other and taught each other and worked as teams in the best way. I answered very few questions, although I didn't stop walking around and checking in with the groups the entire class.
Here are all five.
Tomorrow is test day so today we did review stations. But first, I took up a question from homework that many were doing incorrectly.
A number of students had not put the 5x + 7 in brackets so we talked about how that was not optional. The other brackets you see above were added after when a student asked if you could do that.
Then I explained how review stations work. There were brightly coloured sheets around the room with questions from an old test on them. Students would be randomly paired up (using cards) and each pair would pick up an answer sheet. They would work on the big whiteboards, transfer their answer to the answer sheet, and bring that to me to see whether they were correct. If so, they got a sticker, if not they got to try again. If they were incorrect a second time, then I went over the question with them.
They were so keen! There were a lot of errors but no complaining. They just got back to work and figured things out. Lots of perseverance. There were high fives and hugs. Crazy good.
Given that tomorrow is then end of unit 1, this is the end of my blog posts. I'll still post when I do things that I think are worth sharing, but I think it's clear that I don't do that every day! Thanks for reading :)
We started with this warm up:
This was a challenge for many, but at least as many got the correct answer on the first try. The biggest issue seemed to be that if they did not simplify the fractions before multiplying, the numbers got big fast. And then it was too overwhelming to continue. We spent some more time going over this concept. Hopefully it sticks.
I had noticed some issues with certain homework questions so we tackled those next.
They continued to work on the practice test while I circulated and gave one-on-one help. I had planned on taking it up with them, but time did not allow. I have posted the solutions and hope that they will check their work tonight. We did work on one question together as many students were struggling to start it.
I found it really interesting that using letters actually made the question more approachable for many students. There were simply too many numbers for them to parse through, but once they replaced the bases with x and y, they were able to complete the question.
I also handed out "I can" statements. These are statements written in fairly friendly language that let students self-assess what they know. I'm sorry that the picture below isn't very clear.
Tomorrow we will do review stations!
The sun is shining, the power is on and we had lots of math to do today. We started with this warm up. The intent was to highlight the power of simplifying before multiplying fractions.
I had made an agenda for the day, mostly to keep myself on track, and still managed to go out of order right from the start (sigh).

We jumped into the practice test. I am hoping that seeing the format of a test (3 page booklet) and the types of questions from this past test will help ease some of their anxiety on Friday (test day). I asked them to quietly work on it for 30 minutes. Some skipped questions that they didn't know how to do, while others zipped through it. I did not expect them to complete the test in this time, but wanted to break up the time to allow some conversation and learning to occur. At the end of the 30 minutes, they chose cards to organize themselves into random groups, and went to the big whiteboards to compare answers. There were some really good conversations going on and many misconceptions came to light. Some of the questions could have multiple correct answers so it was great to see them checking each other's work. During this time I circulated and made sure the mathematics was correct and answered questions.
I saved the last 10 minutes of class to talk about vocabulary. I had made a handout for them which we took up.
I think we are making progress. They are willing to talk about their mistakes with classmates and ask questions when things are clear. With a couple more days of review work I hope things will go well on Friday.
Amid power outages due to ridiculously strong winds, we tried to put the material from this unit all together today. We started with the warm up from Friday's group work:
The discussion around this was really interesting and many struggled to correct the work so that the answer was correct.
They spent the next ~30 minutes working through this handout individually. I told them the goal was for each of them to figure out what they still need to work on. We spent the rest of the class working through each of the examples. Other than the vocabulary, we finished it all!